Extended Convergence to Continuous in Probability Processes With Independent Increments

In a previous post, it was seen that all continuous processes with independent increments are Gaussian. We move on now to look at a much more general class of independent increments processes which need not have continuous sample paths. Such processes can be completely described by their jump intensities, a Brownian term, and a deterministic drift component. However, this class of processes is large enough to capture the kinds of behaviour that occur for more general jump-diffusion processes. An important subclass is that of Lévy processes, which have independent and stationary increments. Lévy processes will be looked at in more detail in the following post, and includes as special cases, the Cauchy process, gamma processes, the variance gamma process, Poisson processes, compound Poisson processes and Brownian motion.

Recall that a process ${\{X_t\}_{t\ge0}}$ has the independent increments property if ${X_t-X_s}$ is independent of ${\{X_u\colon u\le s\}}$ for all times ${0\le s\le t}$ . More generally, we say that X has the independent increments property with respect to an underlying filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge0},{\mathbb P})}$ if it is adapted and ${X_t-X_s}$ is independent of ${\mathcal{F}_s}$ for all ${s < t}$ . In particular, every process with independent increments also satisfies the independent increments property with respect to its natural filtration. Throughout this post, I will assume the existence of such a filtered probability space, and the independent increments property will be understood to be with regard to this space.

The process X is said to be continuous in probability if ${X_s\rightarrow X_t}$ in probability as s tends to t. As we now state, a d-dimensional independent increments process X is uniquely specified by a triple ${(\Sigma,b,\mu)}$ where ${\mu}$ is a measure describing the jumps of X, ${\Sigma}$ determines the covariance structure of the Brownian motion component of X, and b is an additional deterministic drift term.

Theorem 1 Let X be an ${{\mathbb R}^d}$ -valued process with independent increments and continuous in probability. Then, there is a unique continuous function ${{\mathbb R}^d\times{\mathbb R}_+\rightarrow{\mathbb C}}$ , ${(a,t)\mapsto\psi_t(a)}$ such that ${\psi_0(a)=0}$ and

$\displaystyle {\mathbb E}\left[e^{ia\cdot (X_t-X_0)}\right]=e^{i\psi_t(a)}$ (1)

for all ${a\in{\mathbb R}^d}$ and ${t\ge0}$ . Also, ${\psi_t(a)}$ can be written as

$\displaystyle \psi_t(a)=ia\cdot b_t-\frac{1}{2}a^{\rm T}\Sigma_t a+\int _{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu(x,s)$ (2)

where ${\Sigma_t}$ , ${b_t}$ and ${\mu}$ are uniquely determined and satisfy the following,

${t\mapsto\Sigma_t}$ is a continuous function from ${{\mathbb R}_+}$ to ${{\mathbb R}^{d^2}}$ such that ${\Sigma_0=0}$ and ${\Sigma_t-\Sigma_s}$ is positive semidefinite for all ${t\ge s}$ .

${t\mapsto b_t}$ is a continuous function from ${{\mathbb R}_+}$ to ${{\mathbb R}^d}$ , with ${b_0=0}$ .

${\mu}$ is a Borel measure on ${{\mathbb R}^d\times{\mathbb R}_+}$ with ${\mu(\{0\}\times{\mathbb R}_+)=0}$ , ${\mu({\mathbb R}^d\times\{t\})=0}$ for all ${t\ge 0}$ and,

$\displaystyle \int_{{\mathbb R}^d\times[0,t]}\Vert x\Vert^2\wedge 1\,d\mu(x,s)<\infty.$ (3)

Furthermore, ${(\Sigma,b,\mu)}$ uniquely determine all finite distributions of the process ${X-X_0}$ .

Conversely, if ${(\Sigma,b,\mu)}$ is any triple satisfying the three conditions above, then there exists a process with independent increments satisfying (1,2).

Equation (2) is an extension of the Lévy-Khintchine formula to inhomogeneous processes. In the case where X has stationary increments (i.e., it is a Lévy process) the statement above simplifies. Then, it is possible to write ${b_t=\tilde b t}$ , ${\Sigma_t=\tilde \Sigma t}$ and ${d\mu(x,t)=d\nu(x)dt}$ for parameters ${\tilde b\in{\mathbb R}^d}$ , ${\Sigma\in{\mathbb R}^{d^2}}$ and measure ${\nu}$ on ${{\mathbb R}^d}$ . In that case, (2) reduces to the standard Lévy-Khintchine formula, which I look at in more detail in the following post. It should be mentioned that the term ${ia\cdot x/(1+\Vert x\Vert)}$ inside the integral in (2) is only there to ensure that the integrand is bounded by a multiple of ${\Vert x\Vert^2\wedge1}$ , so that it is ${\mu}$ -integrable. It could just as easily be replaced by any other bounded term of the form ${ia\cdot x\theta(x)}$ for a function ${\theta(x)\rightarrow1}$ as ${\Vert x\Vert\rightarrow0}$ . For example, the alternative ${ia\cdot x1_{\{\Vert x\Vert\le1\}}}$ is often used instead. Changing this term does not alter the expression (2), with the differences in the integral simply being absorbed into the drift term b. If ${\int_{{\mathbb R}^d\times[0,t]}\Vert x\Vert\wedge1\,d\mu(x,s)}$ is finite, it is often convenient to drop this term completely.

The proof of Theorem 1 will occupy most of this post. For more details on the ideas used in this post see, for example, Kallenberg (Foundations of Modern Probability). Note that, by the independence of the increments of X, equation (1) determines the characteristic function of ${X_t-X_s}$ ,

$\displaystyle {\mathbb E}\left[e^{ia\cdot(X_t-X_s)}\right]= {\mathbb E}\left[e^{ia\cdot(X_t-X_0)}\right]/{\mathbb E}\left[e^{ia\cdot(X_s-X_0)}\right]=e^{ia\cdot(\psi_t(a)-\psi_s(a))},$

for all ${t\ge s}$ . By independence of the increments again, this uniquely determines all the finite distributions of ${X-X_0}$ .

As it is stated, Theorem 1 shows that the parameters ${(\Sigma,b,\mu)}$ uniquely determine the finite distributions of X, since they determine its characteristic function. However, the way in which these terms relate to the paths of the process can be explained in more detail. Roughly speaking, ${\mu}$ describes the intensity of the jumps of X, ${\Sigma}$ describes the covariance structure, and quadratic variation, of its Brownian motion component, and b is an additional drift component.

Theorem 2 Any ${\mathbb{R}^d}$ -valued stochastic process X which is continuous in probability with independent increments has a cadlag modification. If it is assumed that X is cadlag, then ${(\Sigma,b,\mu)}$ as in Theorem 1 are as follows.

The process

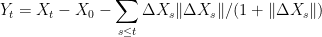
$\displaystyle Y_t=X_t-X_0-\sum_{s\le t}\Delta X_s\Vert\Delta X_s\Vert/(1+\Vert\Delta X_s\Vert)$ (4)

is integrable, and ${b_t={\mathbb E}[Y_t]}$ . Furthermore, ${Y_t-b_t}$ is a martingale.

The process X decomposes uniquely as ${X_t=b_t+W_t+Y_t}$ where W is a continuous centered Gaussian process with independent increments and ${W_0=0}$ , Y is a semimartingale with independent increments whose quadratic variation has zero continuous part, ${[Y^i,Y^j]^c=0}$ . Then, W and Y are independent, Y has parameters ${(0,0,\mu)}$ and

$\displaystyle \Sigma^{ij}_t=[W^i,W^j]_t={\rm Cov}(W^i_t,W^j_t).$ (5)

For any nonnegative measurable ${f\colon{\mathbb R}^d\times{\mathbb R}_+\rightarrow{\mathbb R}}$ ,

$\displaystyle \mu(f)={\mathbb E}\left[\sum_{t>0}1_{\{\Delta X_t\not=0\}}f(\Delta X_t,t)\right].$ (6)

In particular, for any measurable ${A\subseteq{\mathbb R}^d\times{\mathbb R}_+}$ the random variable

$\displaystyle \eta(A)\equiv\sum_{t>0}1_{\{\Delta X_t\not=0,(\Delta X_t,t)\in A\}}$ (7)

is almost surely infinite whenever ${\mu(A)}$ is infinite, and has the Poisson distribution of rate ${\mu(A)}$ otherwise. If ${A_1,\ldots,A_n}$ are disjoint subsets of ${{\mathbb R}^d\times{\mathbb R}_+}$ then ${\eta(A_1),\ldots,\eta(A_n)}$ are independent random variables.

Furthermore, letting ${\mathcal{P}}$ be the predictable sigma-algebra and

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle{\mathbb R}^d\times{\mathbb R}_+\times\Omega\rightarrow{\mathbb R},\smallskip\\ &\displaystyle(x,t,\omega)\mapsto f(x,t)(\omega) \end{array}$

be ${\mathcal{B}({\mathbb R}^d)\otimes\mathcal{P}}$ -measurable such that ${f(0,t)=0}$ and ${\int_{{\mathbb R}^d\times[0,t]}\vert f(x,s)\vert\,d\mu(x,s)}$ is integrable (resp. locally integrable) then,

$\displaystyle M_t\equiv\sum_{s\le t}f(\Delta X_s,s)-\int_{{\mathbb R}^d\times[0,t]}f(x,s)\,d\mu(x,s)$

is a martingale (resp. local martingale).

Along with Theorem 1, the above result will be proven bit-by-bit during this post. In the decomposition of X given in the second statement, the process Y has zero Gaussian component or, equivalently, its quadratic covariations are pure jump processes. The term ${b_t+Y_t}$ is the purely discontinuous part of X and the Gaussian process W is the purely continuous part. More generally, an independent increments process is said to be purely discontinuous if it has parameters ${(0,b,\mu)}$ , so the Brownian motion component is zero. It can be seen from expression (2) for the characteristic function that W has parameters ${(0,\Sigma,0)}$ .

The third statement shows that ${\mu}$ describes the intensity at which the jumps of X occur and, more specifically, shows that they arrive according to the Poisson distribution with rate given by ${\mu}$ . The random variables ${\eta(\cdot)}$ given by equation (7) define a Poisson point process (aka, Poisson random measure). Poisson point processes can be used to construct processes with independent increments. Although I do not explicitly take that approach here, more details can be found in Kallenberg. The final statement shows that the measure ${\mu}$ defines the compensator of the sum ${V_t=\sum_{s\le t}f(\Delta X_s,s)}$ . That is, we can construct a continuous FV process A such that ${V-A}$ is a local martingale.

Let us now move on to proving the main results of this post. Throughout, we assume that the underlying filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge0},{\mathbb P})}$ is complete. We start by showing that cadlag modifications exist. As there is no requirement here for the process X to have stationary increments, it will not in general be a homogeneous Markov process. However, the space-time process ${(X_t,t)}$ will be homogeneous Markov and, in fact, is Feller.

Lemma 3 Let X be an ${\mathbb{R}^d}$ valued process with independent increments and continuous in probability. For each ${t\ge0}$ , define the transition probability ${P_t}$ on ${{\mathbb R}^d\times{\mathbb R}_+}$ by

$\displaystyle P_tf(x,s)={\mathbb E}[f(X_{s+t}-X_s+x,s+t)]$ (8)

for nonnegative measurable ${f\colon{\mathbb R}^d\times{\mathbb R}_+\rightarrow{\mathbb R}}$ .

Then, ${(X_t,t)}$ is a Markov process with Feller transition function ${\{P_t\}_{t\ge0}}$ . In particular, X has a cadlag modification.

Proof: The existence of cadlag modifications is a standard property of Feller processes. So, it just needs to be shown that the specified transition probabilities do indeed define a Feller transition function with respect to which X is a Markov process.

By the independent increments property, (8) can be rewritten as

$\displaystyle P_tf(x,s)={\mathbb E}[f(X_{s+t}-X_s+x,s+t)\mid\mathcal{F}_s],$

(9)

which remains true if x is replaced by an ${\mathcal{F}_s}$ -measurable random variable. To show that this defines a transition function, the Chapman-Kolmogorov equation ${P_tP_u=P_{t+u}}$ needs to be verified,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle P_tP_uf(x,s)&\displaystyle={\mathbb E}[P_uf(X_{s+t}-X_s+x,s+t)]\smallskip\\ &\displaystyle={\mathbb E}\left[{\mathbb E}[f(X_{s+t+u}-X_{s}+x,s+t+u)\mid\mathcal{F}_{s+t}]\right]\smallskip\\ &\displaystyle=P_{t+u}f(x,s). \end{array}$

Here, the second equality is simply using (9) with s+t in place of s and ${X_{s+t}-X_s+x}$ in place of x. Substituting ${X_s}$ in place of x in (9) gives

$\displaystyle P_tf(X_s,s)={\mathbb E}[f(X_{s+t},s+t)\mid\mathcal{F}_s],$

so X is Markov with transition function ${\{P_t\}_{t\ge0}}$ .

Only the Feller property remains. For this it needs to be shown that, for any ${f\in C_0({\mathbb R}^d\times{\mathbb R}_+)}$ then ${P_tf\in C_0({\mathbb R}^d\times{\mathbb R}_+)}$ and ${P_tf\rightarrow f}$ in the pointwise topology as t tends to zero. Recall that ${f\in C_0}$ means that ${f\colon{\mathbb R}^d\times{\mathbb R}_+\rightarrow{\mathbb R}}$ is continuous and ${f(x,t)\rightarrow 0}$ as ${\Vert x\Vert+t\rightarrow\infty}$ . Choosing sequences ${x_n\rightarrow x\in{\mathbb R}^d}$ and ${s_n\rightarrow s\in{\mathbb R}_+}$ , continuity in probability of X and bounded convergence gives

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle P_tf(x_n,s_n)&\displaystyle={\mathbb E}[f(X_{s_n+t}-X_{s_n}+x_n,s_n+t)]\smallskip\\ &\displaystyle\rightarrow{\mathbb E}[f(X_{s+t}-X_s+x,s+t)]=P_tf(x,s). \end{array}$

So ${P_tf}$ is continuous. Similarly, if ${\Vert x_n\Vert+s_n\rightarrow\infty}$ then ${\Vert X_{s_n+t}-X_{s_n}+x_n\Vert+s_n}$ tends to infinity in probability and, again by bounded convergence,

$\displaystyle P_tf(x_n,s_n)={\mathbb E}[f(X_{s_n+t}-X_{s_n}+x_n,s_n+t)]\rightarrow0.$

So ${P_tf\in C_0}$ as required.

Finally, choose ${t_n\rightarrow0}$ . Bounded convergence again gives

$\displaystyle P_{t_n}f(x,s)={\mathbb E}[f(X_{s+t_n}-X_s+x,s+t_n)]\rightarrow f(x,s),$

so that ${\{P_t\}_{t\ge0}}$ is Feller as required. ⬜

So, from now on, it can be assumed that X is cadlag. We can show directly that, as stated in Theorem 1, the jumps of X do indeed occur according to the Poisson distribution with rate determined by ${\mu}$ .

Lemma 4 Let X be a cadlag ${{\mathbb R}^d}$ -valued process with independent increments and continuous in probability. Define the measure ${\mu}$ on ${{\mathbb R}^d\times{\mathbb R}_+}$ by (6) and, for each measurable ${A\subseteq{\mathbb R}^d\times{\mathbb R}_+}$ define the random variable ${\eta(A)}$ by (7).

Proof: It follows directly from the definitions that ${\mu(A)={\mathbb E}[\eta(A)]}$ , so that ${\eta(A)}$ is almost surely finite whenever ${\mu(A)<\infty}$ . Conversely, suppose that ${\eta(A)}$ is almost surely finite. Then we can define the process ${Y^A_t\equiv\eta(A\cap({\mathbb R}^d\times[0,t]))}$ . So, ${Y^A_t}$ is just the number of times ${s\le t}$ at which ${(\Delta X_s,s)}$ is in A. This is a counting process which is continuous in probability and, as ${Y^A_t-Y^A_s}$ depends only on the increments of X in the interval [s,t], it satisfies the independent increments process. Hence, ${Y^A}$ is a Poisson process with cumulative rate ${{\mathbb E}[Y^A_t]=\mu(A\cap({\mathbb R}^d\times[0,t]))}$ . Letting t increase to infinity, we see that ${Y^A_\infty=\eta(A)}$ is Poisson with rate ${\mu(A)}$ , which must therefore be finite.

Now, for any ${\epsilon,t>0}$ the fact that X is cadlag means that, with probability one, ${\Vert\Delta X\Vert}$ can only be greater than ${\epsilon}$ finitely often before time t. So, letting A be the set of ${(x,s)\in{\mathbb R}^d\times{\mathbb R}_+}$ with ${\Vert x\Vert\ge\epsilon}$ and ${s\le t}$ , ${\eta(A)}$ is almost surely finite. As shown above, this implies that ${\mu(A)<\infty}$ .

Next, suppose that ${A\subseteq{\mathbb R}^d\times{\mathbb R}_+}$ is such that ${\mu(A)=\infty}$ . Then there are subsets ${A_n}$ increasing to A with ${\mu(A_n)}$ finite. So, ${\eta(A_n)\le\eta(A)}$ are Poisson of rate ${\mu(A_n)}$ , which increases to infinity as n goes to infinity, implying that ${\eta(A)}$ is almost surely infinite.

Finally, suppose that ${A_1,\ldots,A_n\subseteq{\mathbb R}^d\times{\mathbb R}_+}$ are pairwise disjoint. By taking limits of sets with finite ${\mu}$ -measure, if required, we can restrict to the case where ${\mu(A_k)<\infty}$ . Then, the Poisson processes ${Y^{A_1},\ldots,Y^{A_n}}$ never jump simultaneously and are therefore independent. So, ${\eta(A_k)=Y^{A_k}_\infty}$ are independent random variables. ⬜

We now move on to proving equations (1,2). For this, we recall the following result from Lemma 3 of the post on continuous processes with independent increments.

Lemma 5 Let X be an ${\mathbb{R}^d}$ -valued process with independent increments and continuous in probability. Then, there is a unique continuous function ${{\mathbb R}^d\times{\mathbb R}_+\rightarrow{\mathbb C}}$ , ${(x,t)\mapsto\psi_t(a)}$ with ${\psi_0(a)=0}$ and satisfying equation (1).

Furthermore, ${\exp(ia\cdot X_t-\psi_t(a))}$ is a martingale for each fixed ${a\in{\mathbb R}^d}$ .

In the case of continuous processes, Ito's formula was applied to the logarithm of the martingale ${\exp(ia\cdot X_t-\psi_t(a))}$ to determine ${\psi_t(a)}$ up to a square integrable martingale term (see Lemma 4 of the earlier post). We can do exactly the same thing here using the generalized Ito formula, which applies to all semimartingales.

Lemma 6 Let X be a cadlag ${{\mathbb R}^d}$ -valued process with independent increments and continuous in probability. Then, there is a continuous function ${\tilde b\colon{\mathbb R}_+\rightarrow{\mathbb R}^d}$ such that ${\tilde X_t=X_t-\tilde b_t}$ is a semimartingale. Letting ${\psi_t(a)}$ be as in Lemma 5, the process

$\displaystyle M_t\equiv ia\cdot(X_t-X_0)-\psi_t(a)-\frac12[a\cdot\tilde X]^c_t+\sum_{s\le t}\left(e^{ia\cdot\Delta X_s}-1-ia\cdot\Delta X_s\right)$

is a square integrable martingale.

Proof: We argue in a similar way is in the proof of Lemma 4 from the post on continuous processes with independent increments. In fact, the proof is almost word-for-word the same as that given in the previous post, the main difference here being the use of the generalized Ito formula.

Fix ${a\in{\mathbb R}^d}$ and set ${Y_t=ia\cdot(X_t-X_0)-\psi_t(a)}$ . By the previous lemma, ${U\equiv\exp(Y)}$ is a martingale and, hence, is a semimartingale. So, Ito's lemma implies that ${Y=\log(U)}$ is also a semimartingale. Note that, although the logarithm is not a well-defined twice differentiable function on ${{\mathbb C}^\times}$ , this is true locally (in fact, on every half-plane). So, there is no problem with applying Ito's lemma here.

Taking imaginary parts of Y shows that ${a\cdot X_t-\Im\psi_t(a)}$ is a semimartingale. So, defining the continuous functions ${\tilde b\colon{\mathbb R}_+\rightarrow{\mathbb R}^d}$ by ${b_t^k=\Im\psi_t(e_k)}$ where ${e_k}$ is the unit vector in the k'th dimension, ${\tilde X_t=X_t-b_t}$ is a semimartingale.

Applying the generalized Ito formula to ${U=\exp(Y)}$ gives,

$\displaystyle U_t= 1+\int_0^t U_{s-}\,dY_s+\frac12\int_0^tU_s\,d[Y]^c_s+\sum_{s\le t}(U_s-U_{s-}-U_{s-}\Delta Y_s).$

As ${\Vert U_t\Vert=\vert\exp(-\psi_t(a))\vert}$ , U is uniformly bounded over any finite time interval and, in particular, is a square integrable martingale. Similarly, ${U^{-1}}$ is bounded over finite time intervals, so

$\displaystyle M_t\equiv\int_0^tU^{-1}\,dU=Y_t+\frac12[Y]^c_t+\sum_{s\le t}(e^{\Delta Y_s}-1-\Delta Y_s)$

(10)

is a square integrable martingale.

Now, Y can be written as ${ia\cdot(\tilde X-\tilde X_0)-V}$ for the process

$\displaystyle V_t\equiv\psi_t(a)-ia\cdot\tilde b_t=ia\cdot(\tilde X_t-\tilde X_0)-Y_t,$

which is both a semimartingale and a deterministic process. Hence, V is of finite variation over all finite time intervals. As FV processes do not contribute to continuous parts of quadratic variations,

$\displaystyle [Y]^c=[ia\cdot\tilde X]^c=-[a\cdot\tilde X]^c.$

Substituting this and the definition of Y back into (10) gives the required expression for M. ⬜

Taking expectations of the martingale M defined in Lemma 6 gives us an expression for ${\psi_t(a)}$ which, with a bit of work, gives the proof of Theorem 1 in one direction. Lemma 7 below completes much of the proofs required in this post. It will only remain to prove that the coefficients ${(\Sigma,b,\mu)}$ are uniquely determined by equation (2), that we can construct an independent increments process corresponding to such parameters, and the decomposition given in the second statement of Theorem 2 and the final statement of Theorem 2 also remain to be shown.

Lemma 7 Let X be a cadlag ${{\mathbb R}^d}$ -valued process with independent increments and continuous in probability. Define the following.

The process
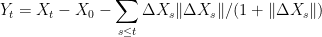
$\displaystyle Y_t=X_t-X_0-\sum_{s\le t}\Delta X_s\Vert\Delta X_s\Vert/(1+\Vert\Delta X_s\Vert)$

is uniformly integrable over finite time intervals, so we can define the continuous function ${b\colon{\mathbb R}_+\rightarrow{\mathbb R}^d}$ by ${b_t={\mathbb E}[Y_t]}$ and, then, ${Y_t-b_t}$ is a martingale.

With b as above, ${\tilde X\equiv X-b}$ is a semimartingale, so we can set

$\displaystyle \Sigma^{ij}_t={\mathbb E}\left[[\tilde X^i,\tilde X^j]^c_t\right].$ (11)

Define the measure ${\mu}$ on ${{\mathbb R}^d\times{\mathbb R}_+}$ by (6).

Then, ${(\Sigma,b,\mu)}$ satisfy the properties stated in Theorem 1 and identity (2) holds.

Proof: Let M be the square integrable martingale defined in Lemma 6. Applying the Ito isometry to the real and imaginary components of M respectively,

$\displaystyle {\mathbb E}\left[\sum_{s\le t}\vert\Delta M_s\vert^2\right]\le{\mathbb E}\left[[\Re M]_t+[\Im M]_t\right]={\mathbb E}\left[\vert M_t\vert^2\right],$

which is finite. However, M has jump ${e^{ia\cdot \Delta X}-1}$ , so that ${\vert\Delta M\vert^2=4\sin^2(a\cdot \Delta X/2)}$ . It follows that

$\displaystyle \int_{{\mathbb R}^d\times[0,t]}\sin^2(a\cdot x/2)\,d\mu(x,s)={\mathbb E}\left[\sum_{s\le t}\sin^2(a\cdot \Delta X_s/2)\right]<\infty.$

Since ${\sin(x)/x\rightarrow1}$ as ${x\rightarrow0}$ we have shown that

$\displaystyle \int_{{\mathbb R}^d\times[0,t]}1_{\{\Vert x\Vert\le1\}}\Vert x\Vert^2\,d\mu(x,s)<\infty.$

Also, Lemma 4 states that ${\mu}$ has finite measure on the set of ${(x,s)}$ with ${\Vert x\Vert\ge1}$ and ${s\le t}$ , giving inequality (3). As ${\mu(\{0\}\times{\mathbb R}_+)=0}$ by definition and ${\mu({\mathbb R}^d\times\{t\})=0}$ by continuity in probability of X, ${\mu}$ satisfies the required properties.

Defining the process Y by (4), we can rearrange the expression for M,

$\displaystyle M_t=ia\cdot Y_t-\frac12[a\cdot\tilde X]^c_t-\psi_t(a)+\sum_{s\le t}\left(e^{ia\cdot\Delta X_s}-1-\frac{ia\cdot\Delta X_s}{1+\Vert\Delta X_s\Vert}\right).$

(12)

The terms inside the summation are bounded and of order ${\Vert\Delta X_s\Vert^2}$ , so are bounded by a multiple of ${\Vert\Delta X_s\Vert^2\wedge 1}$ . So, inequality (3) says that the summation is bounded by an integrable random variable over finite time intervals, so the first two terms of the above expression for M are also bounded by an integrable random variable. Taking the real and imaginary parts shows that Y and ${[a\cdot\tilde X]}$ are also bounded by an integrable random variable over any finite time interval. So, we can define

$\displaystyle b_t={\mathbb E}[Y_t],\ \Sigma^{jk}_t={\mathbb E}\left[[\tilde X^j,\tilde X^k]^c\right]$

which, by dominated convergence, are continuous. As ${a^{\rm T}\Sigma_ta={\mathbb E}[[a\cdot\tilde X]^c_t]}$ is increasing, ${\Sigma_t-\Sigma_s}$ is positive semidefinite for all ${t\ge s}$ . So, we have shown that ${b_t,\Sigma_t}$ satisfy the required properties.

Taking expectations of (12),

$\displaystyle 0=ia\cdot b_t-\frac12a^{\rm T}\Sigma_t-\psi_t(a)+\int_{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu(x,s)$

giving equation (2) for ${\psi_t(a)}$ .

Finally, note that ${Y-b}$ is an integrable process with zero mean and independent increments, so is a martingale. Then ${X-b}$ is the sum of the martingale ${Y-b}$ and an FV process, so is a semimartingale. Recall also, from Lemma 6, that ${\tilde X}$ was defined to be ${X-\tilde b}$ for any continuous deterministic process ${\tilde b}$ making ${\tilde X}$ into a semimartingale, so we may as well take ${\tilde b=b}$ . ⬜

This almost completes the proof of Theorem 1. Other than constructing the process X from ${(\Sigma,b,\mu)}$ , which will be done below, it only remains to show that ${(\Sigma,b,\mu)}$ are uniquely determined by the identity (2). This will follow from the fact that any different set of parameters ${(b^\prime,\Sigma^\prime,\mu^\prime)}$ give rise to a different process, using the construction described below. However, (2) can also be inverted by applying a Fourier transform. If ${f\colon{\mathbb R}^d\rightarrow{\mathbb R}}$ is a Schwartz function, then integrating (2) against its Fourier transform ${\hat f(a)=(2\pi)^d\int f(x)e^{-ix\cdot a}\,dx}$ gives,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle\int\psi_t(a)\hat f(a)\,da =&\displaystyle b^j_tf_j(0)+\frac12\Sigma_t^{jk}f_{jk}(0)\smallskip\\ &\displaystyle\quad+\int_{{\mathbb R}^d\times[0,t]}\left(f(x)-f(0)-\frac{x_jf_j(0)}{1+\Vert x\Vert}\right)\,d\mu(x,s) \end{array}$

(13)

Here, ${f_j}$ and ${f_{jk}}$ represent the partial derivatives of f, and summation over the indices j, k is understood. If f is zero in a neighbourhood of the origin, then (13) reduces to ${\int_{{\mathbb R}^d\times[0,t]}f\,d\mu}$ , so it uniquely determines ${\mu}$ . Then, ${b}$ and ${\Sigma}$ can be read off from (13).

We now prove the final statement of Theorem 2, which constructs the compensator of a sum over the jumps of an independent increments process in terms of the measure ${\mu}$ .

Lemma 8 Let X be a d-dimensional cadlag independent increments process with ${(\Sigma,b,\mu)}$ as in Theorem 1 and let

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle{\mathbb R}^d\times{\mathbb R}_+\times\Omega\rightarrow{\mathbb R},\smallskip\\ &\displaystyle(x,t,\omega)\mapsto f(x,t)(\omega) \end{array}$

be ${\mathcal{B}({\mathbb R}^d)\otimes\mathcal{P}}$ -measurable such that ${f(0,t)=0}$ and ${\int_{{\mathbb R}^d\times[0,t]}\vert f(x,s)\vert\,d\mu(x,s)}$ is integrable (resp. locally integrable). Then,

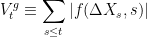
$\displaystyle V^g_t\equiv\sum_{s\le t}\vert f(\Delta X_s,s)\vert$

is integrable (resp. locally integrable) and

$\displaystyle M^f_t\equiv\sum_{s\le t}f(\Delta X_s,s)-\int_{{\mathbb R}^d\times[0,t]}f(x,s)\,d\mu(x,s)$

is a martingale (resp. local martingale).

Proof: Choose an ${\epsilon > 0}$ . If ${\vert f\vert\le K}$ for some constant K and ${f(x,t)=0}$ for ${\Vert x\Vert<\epsilon}$ then (6) gives

$\displaystyle {\mathbb E}\left[V^f_t\right]\le K\int_{{\mathbb R}^d\times[0,t]}1_{\{\Vert x\Vert\ge\epsilon\}}\,d\mu(x,s)$

which, by (3), is finite.

First, consider f of the form ${f(x,t)=g(x)}$ for some bounded measurable ${g\colon{\mathbb R}^d\rightarrow{\mathbb R}}$ with ${g(x)=0}$ for ${\Vert x\Vert <\epsilon}$ . Then, by (6),

$\displaystyle M^f_t=\sum_{s\le t}g(\Delta X_s)-\int_{{\mathbb R}^d\times[0,t]}g(x)\,d\mu(x,s)$

has zero mean. Also, ${M^f_t-M^f_s}$ is a function of ${\{\Delta X_u\}_{u\in(s,t]}}$ and, therefore, is independent of ${\mathcal{F}_s}$ . So, ${M^f}$ is a martingale.

Next, consider ${f(x,t)=\xi_tg(x)}$ where ${\xi}$ is a bounded predictable process and g is as above. Setting ${\tilde f(x,t)=g(x)}$ gives

$\displaystyle M^f_t=\int_0^t\xi_s\,dM^{\tilde f}_s.$

As stochastic integration preserves the local martingale property this is a local martingale and, as it has integrable variation over finite time intervals, it will be a proper martingale. The idea is to apply the functional monotone class theorem to extend this to all bounded f with ${f(x,t)=0}$ for ${\Vert x\Vert <\epsilon}$ . Linearity is clear. That is, if ${M^{f_1},M^{f_2}}$ are martingales then ${M^{f_1+f_2}=M^{f_1}+M^{f_2}}$ are martingales and, for a constant ${\lambda}$ , ${M^{\lambda f_1}=\lambda M^{f_1}}$ is a martingale.

Now consider a sequence ${f_n}$ of nonnegative ${\mathcal{B}({\mathbb R}^d)\otimes\mathcal{P}}$ -measurable functions increasing to a limit f such that ${M^{f_n}}$ are martingales, ${f(0,t)=0}$ , and that ${\int_{{\mathbb R}^d\times[0,t]}f\,d\mu}$ is integrable. By monotone convergence,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[V^f_t\right]&\displaystyle=\lim_{n\rightarrow\infty}{\mathbb E}\left[V^{f_n}_t\right]=\lim_{n\rightarrow\infty}{\mathbb E}\left[\int_{{\mathbb R}^d\times[0,t]}f_n\,d\mu\right]\smallskip\\ &\displaystyle={\mathbb E}\left[\int_{{\mathbb R}^d\times[0,t]}f\,d\mu\right]. \end{array}$

This shows that ${V^f}$ is integrable and ${M^{f_n}_t=V^{f_n}_t-\int_{{\mathbb R}^d\times[0,t]}f_n\,d\mu}$ converges to ${M^f_t}$ in ${L^1}$ . So, ${M^f}$ is a martingale. By the functional monotone class theorem, this implies that ${M^f}$ is a martingale for all bounded ${\mathcal{B}({\mathbb R}^d)\otimes\mathcal{P}}$ -measurable functions f with ${f(x,t)=0}$ for ${\Vert x\Vert < \epsilon}$ .

Now suppose that f is ${\mathcal{B}({\mathbb R}^d)\otimes\mathcal{P}}$ -measurable with ${f(0,t)=0}$ and that ${\int_{{\mathbb R}^d\times[0,t]}\vert f\vert\,d\mu}$ is integrable. Writing f as the difference of its positive and negative parts, we can reduce the problem to nonnegative f. However, in that case, the functions ${f_n(x,t)\equiv1_{\{\Vert x\Vert\ge1/n\}}n\wedge f(x,t)}$ increase to f. As shown above, ${V^{f_n}}$ are integrable, ${M^{f_n}}$ are martingales, and ${V^{f_n}_t\rightarrow V^f_t}$ and ${M^{f_n}_t\rightarrow M^f_t}$ in ${L^1}$ . So, ${V^f}$ is integrable and ${M^f}$ is a martingale.

Finally, suppose that ${f(0,t)=0}$ and ${W_t\equiv\int_{{\mathbb R}^d\times[0,t]}\vert f\vert\,d\mu}$ is locally integrable. Choose stopping times ${\tau_n}$ increasing to infinity such that the stopped process ${W^{\tau_n}}$ is integrable. Then, setting ${f_n(x,t)=1_{\{t\le\tau_n\}}f(x,t)}$ , ${\int_{{\mathbb R}^d\times[0,t]}\vert f_n\vert\,d\mu=W^{\tau_n}_t}$ is integrable. So, by the above, ${(V^f)^{\tau_n}=V^{f_n}}$ is integrable and ${(M^f)^{\tau_n}=M^{f_n}}$ is a martingale. ⬜

Constructing independent increments processes

Having proven that equation (2) holds for an independent increments process X, it remains to construct the process given parameters ${(\Sigma,b,\mu)}$ . In the case where ${\mu=0}$ then (2) shows that X will be Gaussian, and can be constructed as described in the post on continuous independent increments processes. We, therefore, concentrate on the purely discontinuous case. Then, from Lemma 4 we know precisely how the jumps of X are distributed. So, to reconstruct X, the method is clear enough. We just generate its jumps ${\Delta X}$ according to the Poisson distributions described above, then sum these up to obtain X. However, there is one problem. The process X can have infinitely many jumps over any finite time interval and, in fact, the sum of their absolute values can be infinite (as is the case for the Cauchy process, for example). So, the result of the sum ${\sum\Delta X_s}$ will depend on the order of summation. We avoid these issues by starting with the case where the jump measure ${\mu}$ is finite, so the process has only finitely many jumps.

Lemma 9 Let ${\mu}$ be a finite measure on ${{\mathbb R}^d\times{\mathbb R}_+}$ such that ${\mu(\{0\}\times{\mathbb R}_+)=0}$ and ${\mu({\mathbb R}^d\times\{t\})=0}$ for every ${t\ge0}$ .

Let ${(Z_1,T_1),(Z_2,T_2),\ldots}$ be a sequence of independent ${{\mathbb R}^d\times{\mathbb R}_+}$ -valued random variables with distribution ${\bar\mu=\mu/\mu(1)}$ , and N be an independent Poisson distributed random variable of rate ${\mu(1)}$ . Setting,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle X_t\equiv\sum_{n=1}^N1_{\{T_n\le t\}}Z_n-b_t,\smallskip\\ &\displaystyle b_t\equiv\int_{{\mathbb R}^d\times[0,t]}\frac{x}{1+\Vert x\Vert}\,d\mu(x,s), \end{array}$

then X is an independent increments process with parameters ${(0,0,\mu)}$ .

Proof: We can prove this by a direct computation of the characteristic function of the increments of X and then comparing with (2).

Fix any times ${0=t_0<t_1<\cdots<t_m=\infty}$ and let ${N_k=\vert\{T_1,\ldots,T_N\}\cap(t_{k-1},t_k]\vert}$ and ${Y_t=\sum_{n=1}^N1_{\{T_n\le t\}}Z_n}$ . Independence of the variables ${(Z_n,T_n)}$ conditional on N gives

$\displaystyle {\mathbb E}\left[\exp\left(\sum_{k=1}^mia_k\cdot(Y_{t_k}-Y_{t_{k-1}})\right)\right] ={\mathbb E}\left[\prod_{k=1}^m{\mathbb E}[\exp(ia_k\cdot(Y_{t_k}-Y_{t_{k-1}})\mid N_k]\right]$

for any ${a_1,\ldots,a_m\in{\mathbb R}^d}$ . Then, noting that, conditional on ${N_k}$ , ${Y_{t_k}-Y_{t_{k-1}}}$ is the sum of ${N_k}$ independent random variables with distribution given by ${\mu}$ ,

$\displaystyle {\mathbb E}[\exp(ia_k\cdot(Y_{t_k}-Y_{t_{k-1}}))\mid N_k]=\left(\frac{1}{\mu(A_k)}\int_{A_k}e^{ia_k\cdot x}\,d\mu(x,s)\right)^{N_k}.$

where ${A_k={\mathbb R}^d\times(t_{k-1},t_k]}$ . Writing the right hand side of this as ${c_k^{N_k}}$ for brevity, we can use the fact that, conditional on N, ${(N_1,\ldots,N_m)}$ has the multinomial distribution to get

$\displaystyle {\mathbb E}\left[\prod_{k=1}^mc_k^{N_k}\right]={\mathbb E}\left[\sum_{n_1+\cdots+n_m=N}\frac{N!}{n_1!\cdots n_m!}\prod_{k=1}^m\bar\mu(A_k)^{n_k}\prod_{k=1}^mc_k^{n_k}\right].$

By the Poisson distribution, the probability that N equals any nonnegative integer n is ${e^{-\mu(1)}\mu(1)^n/n!}$ giving,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[\prod_{k=1}^mc_k^{N_k}\right]&\displaystyle=\sum_{n=0}^{\infty}e^{-\mu(1)}\frac{\mu(1)^n}{n!}\sum_{n_1+\cdots+n_m=n}\frac{n!}{n_1!\cdots n_m!}\prod_{k=1}^m(\bar\mu(A_k)c_k)^{n_k} \smallskip\\ &\displaystyle=\prod_{k=1}^m\sum_{n_k=0}^\infty\frac{e^{-\mu(A_k)}}{n_k!}(\mu(A_k)c_k)^{n_k}\smallskip\\ &\displaystyle=\prod_{k=1}^me^{\mu(A_k)(c_k-1)}\smallskip\\ &\displaystyle=\exp\left(\sum_{k=1}^m\int_{A_k}(e^{ia_k\cdot x}-1)\,d\mu(x,s)\right). \end{array}$

So, the characteristic function of ${(Y_{t_1}-Y_{t_0},\ldots,Y_{t_m}-Y_{t_{m-1}})}$ is the product of the characteristic functions of the increments ${Y_{t_k}-Y_{t_{k-1}}}$ , showing that Y is an independent increments process. The characteristic function of ${X_t}$ is then,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[e^{ia\cdot X_t}\right]&\displaystyle={\mathbb E}\left[e^{ia\cdot Y_t}\right]e^{-ia\cdot b_t}\smallskip\\ &\displaystyle=\exp\left(\int_{{\mathbb R}^d\times[0,t]}(e^{ia\cdot x}-1)\,d\mu(x,s)\right)e^{-ia\cdot b_t}\smallskip\\ &\displaystyle=\exp\left(\int_{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu(x,s)\right). \end{array}$

Comparing with (2) we see that this is of the correct form. ⬜

Lemma 9 needs to be extended to cope with processes with infinitely many jumps. This can be done by writing such a process as an infinite sum of processes, each with finitely many jumps, and convergence can be determined by looking at the explicit expressions for their characteristic functions.

Lemma 10 Let ${\mu_1,\mu_2,\ldots}$ be measures on ${{\mathbb R}^d\times{\mathbb R}_+}$ such that ${\mu=\sum_n\mu_n}$ satisfies the conditions of Theorem 1.

Also, let ${X^{(1)},X^{(2)},\ldots}$ be a sequence of independent processes such that ${X^{(k)}}$ is an ${{\mathbb R}^d}$ -valued independent increments process with parameters ${(0,0,\mu_k)}$ and ${X^{(k)}_0=0}$ . Then,

$\displaystyle X_t=\sum_{k=1}^\infty X^{(k)}_t$

converges in probability to the independent increments process X with parameters ${(0,0,\mu)}$ .

Proof: Let us set ${Y^{(n)}_t=\sum_{k=1}^nX^{(k)}_t}$ . As a sum of the independent processes ${X^{(k)}}$ , each of which has the independent increments property, it follows that ${Y^{(n)}}$ satisfy the independent increments property. We just need to show that they converge to the process X. For any ${m\ge n}$ , independence of the processes ${X^{(k)}_t}$ gives

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[e^{ia\cdot(Y^{(m)}_t-Y^{(n)}_t)}\right]&\displaystyle=\prod_{k=n+1}^m{\mathbb E}\left[e^{ia\cdot X^{(k)}_t}\right]\smallskip\\ &\displaystyle=\exp\left(\sum_{k=n+1}^m\int_{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu_k(x,s)\right) \end{array}$

The integrand on the right hand side is bounded by ${K(\Vert x\Vert^2\wedge1)}$ for some constant K and, therefore, the exponent is bounded by

$\displaystyle K\sum_{k=n+1}^m\int_{{\mathbb R}^d\times[0,t]}\Vert x\Vert^2\wedge1\,d\mu_k(x,s) \le\int_{{\mathbb R}^d\times[0,t]}\Vert x\Vert^2\wedge1\,d\mu(x,s)<\infty.$

By dominated convergence, this goes to zero as m, n go to infinity. So, ${{\mathbb E}[e^{ia\cdot(Y^{(m)}_t-Y^{(n)}_t)}]}$ goes to zero. Therefore, ${Y^{(m)}_t-Y^{(n)}_t}$ tend to zero in probability and, by completeness of ${L^0}$ , the sequence ${Y^{(n)}_t}$ converges in probability to a limit ${X_t}$ . By dominated convergence,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[e^{ia\cdot X_t}\right]&\displaystyle=\lim_{n\rightarrow\infty}{\mathbb E}\left[e^{ia\cdot Y^{(n)}_t}\right]\smallskip\\ &\displaystyle=\lim_{n\rightarrow\infty}\exp\left(\sum_{k=1}^n\int_{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu_k(x,s)\right)\smallskip\\ &\displaystyle=\exp\left(\int_{{\mathbb R}^d\times[0,t]}\left(e^{ia\cdot x}-1-\frac{ia\cdot x}{1+\Vert x\Vert}\right)\,d\mu(x,s)\right) \end{array}$

as required. ⬜

Putting this together, we can use Lemma 9 to construct independent increments processes with finitely many jumps and, then, by summing these, we obtain an independent increments process with arbitrary jump measure ${\mu}$ . Adding on the drift term and Gaussian component gives the process X as required, completing the proof of Theorem 1.

Lemma 11 Let ${(\Sigma,b,\mu)}$ satisfy the conditions of Theorem 1 and define the following.

Then,

$\displaystyle X_t\equiv b_t+W_t+Y_t$

is an independent increments process with parameters ${(\Sigma,b,\mu)}$ .

Proof: This is just a direct application of Lemma 10, and expression (1) follows from the independence of W and Y and the characteristic function of ${b_t+W_t\sim N(b_t,\Sigma_t)}$ ,

$\displaystyle {\mathbb E}\left[e^{ia\cdot(b_t+W_t)}\right]=\exp\left(ia\cdot b_t-\frac12a^{\rm T}\Sigma_ta\right).$

⬜

It only remains to prove the decomposition of X given in the second statement of Theorem 2. We do this now, by making use of the construction given above.

Lemma 12 Let X be a cadlag independent increments process with parameters ${(\Sigma,b,\mu)}$ and, for each ${k\ge 1}$ let ${A_k\subseteq{\mathbb R}^d\times{\mathbb R}_+}$ be as in (14), so that ${\mu(A_k)<\infty}$ . Setting

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle X^{(k)}_t=\sum_{s\ge0}1_{\{(\Delta X_s,s)\in A_k\setminus A_{k-1},s\le t\}}\Delta X_s-\tilde b^n_t,\smallskip\\ &\displaystyle \tilde b^n_t=\int_{A_n\setminus A_{n-1}}\frac{1_{\{s\le t\}}x}{1+\Vert x\Vert}\,d\mu(x,s), \end{array}$ (15)

the sum

$\displaystyle Y_t=\sum_{k=1}^\infty X^{(k)}_t$

converges in probability, and Y is an independent increments process with parameters ${(0,0,\mu)}$ . Furthermore, X decomposes as a sum of independent processes

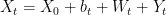
$\displaystyle X_t=X_0+b_t+W_t+Y_t$

where W is an independent increments process possessing a continuous modification and ${W_t-W_s\sim N(0,\Sigma_t-\Sigma_s)}$ for all ${t\ge s}$ .

Proof: First, replacing X by ${X-X_0}$ if necessary, we suppose that ${X_0=0}$ . As the distribution of X is fully determined by ${(\Sigma,b,\mu)}$ , we may as well suppose that X has been constructed according to Lemma 11. It then only needs to be shown that the processes ${X^{(k)}}$ defined in Lemma 11 satisfy (15). First, by the construction given in Lemma 9 for independent increments processes with parameters ${(0,0,1_{A_k\setminus A_{k-1}}\cdot\mu)}$ we see that ${(\Delta X^{(k)}_t,t)\in A_k\setminus A_{k-1}}$ whenever ${\Delta X^{(k)}_t\not=0}$ and,

$\displaystyle X^{(k)}_t=\sum_{s\le t}\Delta X^{(k)}_s-\tilde b^k_t.$

(16)

Next, by Lemma 10 the process ${Y-X^{(k)}=\sum_{j\not=k}X^{(j)}}$ has independent increments with parameters ${(0,0,\nu)}$ where

$\displaystyle \nu=\sum_{j\not=k}1_{A_j\setminus A_{j-1}}\cdot\mu=\mu-1_{A_k\setminus A_{k-1}}\cdot\mu.$

As ${\nu(A_k\setminus A_{k-1})=0}$ , the jumps ${(\Delta Y_t-\Delta X^{(k)}_t,t)}$ are never in ${A_k\setminus A_{k-1}}$ , so we can rewrite (16) as,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle X^{(k)}_t&\displaystyle=\sum_{s\le t}1_{\{(\Delta Y_s,s)\in A_k\setminus A_{k-1}\}}\Delta Y_s-\tilde b^k_s \smallskip\\ &\displaystyle=\sum_{s\le t}1_{\{(\Delta X_s,s)\in A_k\setminus A_{k-1}\}}\Delta X_s-\tilde b^k_s. \end{array}$

⬜

This just about completes the proof of all the statements above. Only one small point remains — in Theorem 2 it was stated that the decomposition ${X=X_0+b+W+Y}$ into a continuous centered Gaussian process W and independent increments process Y with ${[Y^i,Y^j]^c=0}$ is unique. That the process Y given by Lemma 12 has quadratic variation with zero continuous part follows from equation (11) and the fact that it has parameters ${(0,0,\mu)}$ . Uniqueness follows from the fact that if ${X=X_0+b+W^\prime+Y^\prime}$ is any other such decomposition then ${Y^\prime-Y=W-W^\prime}$ is continuous. As ${Y,Y^\prime}$ are both purely discontinuous independent increments processes with the same jumps, the construction above shows that they are equal.